![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)
Next: 2.5 Mapping
Up: 2 Designing Parallel Algorithms
Previous: 2.3 Communication
In the first two stages of the design process, we partitioned the
computation to be performed into a set of tasks and introduced
communication to provide data required by these tasks. The resulting
algorithm is still abstract in the sense that it is not specialized
for efficient execution on any particular parallel computer. In fact,
it may be highly inefficient if, for example, it creates many more
tasks than there are processors on the target computer and this
computer is not designed for efficient execution of small tasks.
In the third stage, agglomeration, we move from the abstract
toward the concrete. We revisit decisions made in the partitioning
and communication phases with a view to obtaining an algorithm that
will execute efficiently on some class of parallel computer. In
particular, we consider whether it is useful to combine, or
agglomerate, tasks identified by the partitioning phase, so as to
provide a smaller number of tasks, each of greater size
(Figure 2.11). We also determine whether it is worthwhile
to replicate
data and/or computation.
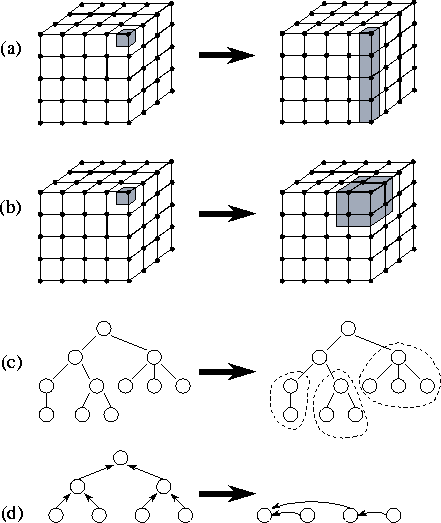
Figure 2.11: Examples of agglomeration. In (a), the size of tasks is
increased by reducing the dimension of the decomposition from three to
two. In (b), adjacent tasks are combined to yield a three-dimensional
decomposition of higher granularity. In (c), subtrees in a
divide-and-conquer structure are coalesced. In (d), nodes in a tree
algorithm are combined.
The number of tasks yielded by the agglomeration phase, although
reduced, may still be greater than the number of processors. In this
case, our design remains somewhat abstract, since issues relating to
the mapping of tasks to processors remain unresolved. Alternatively,
we may choose during the agglomeration phase to reduce the number of
tasks to exactly one per processor. We might do this, for example,
because our target parallel computer or program
development environment demands an SPMD program. In this case, our
design is already largely complete, since in defining P
tasks
that will execute on P
processors, we have also addressed the
mapping problem. In this section, we focus on general issues that
arise when
increasing task granularity. Specific issues relating to the
generation of SPMD programs are discussed in Section 2.5.
Three sometimes-conflicting goals guide decisions concerning
agglomeration and replication: reducing communication costs by
increasing computation and communication granularity, retaining
flexibility
with respect to scalability and mapping
decisions, and reducing software engineering
costs. These
goals are discussed in the next three subsections.
In the partitioning phase of the design process, our efforts are
focused on defining as many tasks as possible. This is a useful
discipline because it forces us to consider a wide range of
opportunities for parallel execution. We note, however, that defining
a large number of fine-grained tasks does not necessarily produce an
efficient parallel algorithm.
One critical issue influencing parallel performance is communication
costs. On most parallel computers, we have to stop computing in order
to send and receive messages. Because we typically would rather be
computing, we can improve performance by reducing the amount of time
spent communicating. Clearly, this performance improvement can be
achieved by sending less data. Perhaps less obviously, it can also be
achieved by using fewer messages, even if we send the same amount of
data. This is because each communication incurs not only a cost
proportional to the amount of data transferred but also a fixed
startup cost. These issues are discussed in detail in
Chapter 3, where we use analytic models to quantify
communication costs.
In addition to communication costs, we may need to be concerned with
task creation costs. For example, the performance of the fine-grained
search algorithm illustrated in Figure 1.13, which creates
one task for each search tree node, is sensitive to task creation
costs.
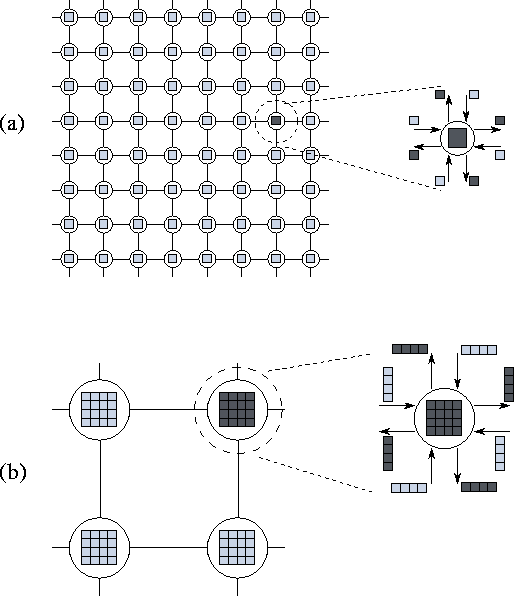
Figure 2.12: Effect of increased granularity on communication costs in
a two-dimensional finite difference problem with a five-point stencil.
The figure shows fine- and coarse-grained two-dimensional partitions
of this problem. In each case, a single task is exploded to show its
outgoing messages (dark shading) and incoming messages (light
shading). In (a), a computation on an 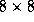 grid is partitioned
into
grid is partitioned
into 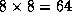 tasks, each responsible for a single point, while
in (b) the same computation is partioned into
tasks, each responsible for a single point, while
in (b) the same computation is partioned into 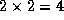 tasks, each
responsible for 16 points. In (a),
tasks, each
responsible for 16 points. In (a), 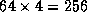 communications
are required, 4 per task; these transfer a total of 256 data values.
In (b), only
communications
are required, 4 per task; these transfer a total of 256 data values.
In (b), only 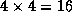 communications are required, and only
communications are required, and only
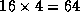 data values are transferred.
data values are transferred.
If the number of communication partners per task is small, we can
often reduce both the number of communication operations and the total
communication volume by increasing the granularity of our
partition, that is, by agglomerating several tasks into one. This
effect is illustrated in Figure 2.12. In this figure, the
reduction in communication costs is due to a surface-to-volume
effect
. In other words, the communication requirements of a task
are proportional to the surface of the subdomain on which it operates,
while the computation requirements are proportional to the subdomain's
volume. In a two-dimensional problem, the ``surface'' scales with the
problem size while the ``volume'' scales as the problem size squared.
Hence, the amount of communication performed for a unit of computation
(the
communication/computation ratio
) decreases as task size
increases. This effect is often visible when a partition is obtained
by using domain decomposition techniques.
A consequence of surface-to-volume effects is that higher-dimensional
decompositions are typically the most efficient, other things being
equal, because they reduce the surface area (communication) required for a
given volume (computation). Hence, from the viewpoint of efficiency
it is usually best to increase granularity by agglomerating tasks in
all dimensions rather than reducing the dimension of the
decomposition. This issue is explored quantitatively in
Example 3.4 in Chapter 3.
The design of an efficient agglomeration strategy can be difficult in
problems with unstructured communications, such as the finite element
problem of Figure 2.9. Specialized techniques that can be
used in such cases are discussed in Section 2.5.1.
We can sometimes trade off replicated computation for reduced
communication requirements and/or execution time. For an example, we
consider a variant of the summation problem presented in
Section 2.3.2, in which the sum must be replicated in
each of the N
tasks that contribute to the sum.
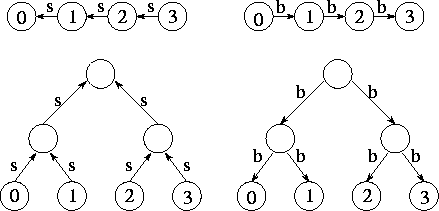
Figure 2.13: Using an array (above) and a tree (below) to perform a
summation and a broadcast. On the left are the communications
performed for the summation (s); on the right, the communications
performed for the broadcast (b). After 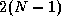 or
or 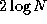 steps,
respectively, the sum of the N values is replicated in each of the
N tasks.
steps,
respectively, the sum of the N values is replicated in each of the
N tasks.
A simple approach to distributing the sum is first to use either a
ring- or tree-based algorithm to compute the sum in a single task, and
then to broadcast
the sum to each of the
N
tasks. The broadcast can be performed using the same
communication structure as the summation; hence, the complete
operation can be performed in either 2(N-1)
or  steps,
depending on which communication structure is used
(Figure 2.13).
steps,
depending on which communication structure is used
(Figure 2.13).
These algorithms are optimal in the sense that they do not perform any
unnecessary computation or communication. However, there also exist
alternative algorithms that execute in less elapsed time, although at
the expense of unnecessary (replicated) computation and communication.
The basic idea is to perform multiple summations concurrently, with
each concurrent summation producing a value in a different task.
We first consider a variant of the array summation algorithm based on
this idea. In this variant, tasks are connected in a ring
rather than an array, and all N
tasks execute the same algorithm
so that N
partial sums are in motion simultaneously. After
N-1
steps, the complete sum is replicated in every task. This
strategy avoids the need for a subsequent broadcast operation, but at
the expense of 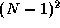 redundant additions and
redundant additions and 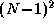 unnecessary communications. However, the summation and broadcast
complete in N-1
rather than 2(N-1)
steps. Hence, the
strategy is faster if the processors would otherwise be idle waiting
for the result of the summation.
unnecessary communications. However, the summation and broadcast
complete in N-1
rather than 2(N-1)
steps. Hence, the
strategy is faster if the processors would otherwise be idle waiting
for the result of the summation.
The tree summation algorithm can be modified in a similar way to avoid
the need for a separate broadcast. That is, multiple tree summations
are performed concurrently so that after 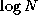 steps each task has
a copy of the sum. One might expect this approach to result in
steps each task has
a copy of the sum. One might expect this approach to result in
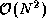 additions and communications, as in the ring algorithm.
However, in this case we can exploit redundancies in both computation
and communication to perform the summation in just
additions and communications, as in the ring algorithm.
However, in this case we can exploit redundancies in both computation
and communication to perform the summation in just 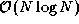 operations. The resulting communication structure, termed a
butterfly, is illustrated in Figure 2.14. In each of the
operations. The resulting communication structure, termed a
butterfly, is illustrated in Figure 2.14. In each of the
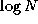 stages, each task receives data from two tasks, performs a
single addition, and sends the result of this addition to two tasks in
the next stage.
stages, each task receives data from two tasks, performs a
single addition, and sends the result of this addition to two tasks in
the next stage.
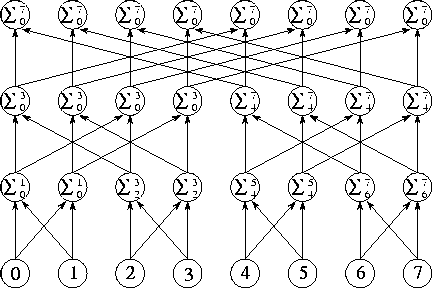
Figure 2.14: The butterfly communication structure
can be used to sum N
values in 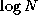 steps. Numbers located
in the bottom row of tasks are propagated up through
steps. Numbers located
in the bottom row of tasks are propagated up through  intermediate stages, thereby producing the complete sum in each task
in the top row.
intermediate stages, thereby producing the complete sum in each task
in the top row.
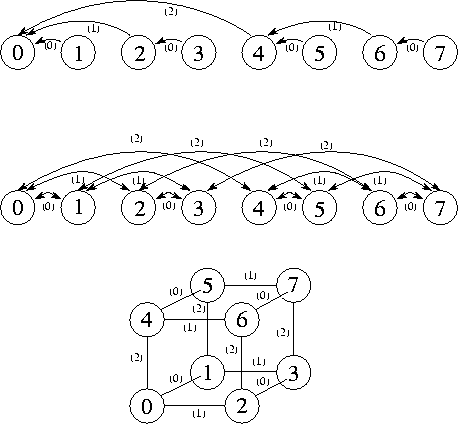
Figure 2.15: The communication structures that result when tasks at
different levels in a tree or butterfly structure are agglomerated.
From top to bottom: a tree, a butterfly, and an equivalent
representation of the butterfly as a hypercube. In each case,
N=8
, and each channel is labeled with the step in which it is
used for communication.
Agglomeration is almost always beneficial if analysis of communication
requirements reveals that a set of tasks cannot execute concurrently.
For example, consider the tree and butterfly structures illustrated in
Figures 2.8 and 2.14. When a single summation
problem is performed, only tasks at the same level in the tree or
butterfly can execute concurrently. (Notice, however, that if many
summations are to be performed, in principle all tasks can be kept
busy by pipelining multiple summation operations.) Hence, tasks at
different levels can be agglomerated without reducing opportunities
for concurrent execution, thereby yielding the communication
structures represented in Figure 2.15. The hypercube
structure shown in this figure is a fundamental communication
structure that has many applications in parallel computing. It is
discussed in greater detail in Chapter 11.
It is easy when agglomerating tasks to make design decisions that
limit unnecessarily an algorithm's scalability. For example, we might
choose to decompose a multidimensional data structure in just a single
dimension, reasoning that this provides more than enough concurrency
for the number of processors available. However, this strategy is
shortsighted if our program must ultimately be ported to larger
parallel computers. It may also lead to a less efficient algorithm,
as discussed in Section 2.4.1.
The ability to create a varying number of tasks is critical if a
program is to be portable and scalable. As discussed in
Chapter 1, good parallel algorithms are designed to be
resilient to changes in processor count. This flexibility can also be
useful when tuning a code for a particular computer. If tasks often
block waiting for remote data, it can be advantageous to map several
tasks to a processor. Then, a blocked task need not result in a
processor becoming idle, since another task may be able to execute in
its place. In this way, one task's communication is overlapped with
another task's computation. This technique, termed overlapping
computation and communication, is discussed in
Chapter 3.
A third benefit of creating more tasks than processors is that doing so
provides greater scope for mapping strategies that balance
computational load over available processors. As a general rule of
thumb, we could require that there be at least an order of magnitude
more tasks than processors. This issue is discussed in the next
section.
The optimal number of tasks is typically best determined by a
combination of analytic modeling and empirical studies. Flexibility
does not necessarily require that a design always create a large
number of tasks. Granularity can be controlled by a compile-time or
runtime parameter. What is important is that a design not incorporate
unnecessary limits on the number of tasks that can be created.
So far, we have assumed that our choice of agglomeration strategy is
determined solely by a desire to improve the efficiency and
flexibility of a parallel algorithm. An additional concern, which can
be particularly important when parallelizing existing sequential
codes, is the relative development costs associated with different
partitioning strategies. From this perspective, the most interesting
strategies may be those that avoid extensive code changes. For
example, in a code that operates on a multidimensional grid, it may be
advantageous to avoid partitioning altogether in one dimension, if
doing so allows existing routines to be reused unchanged in a parallel
program.
Frequently, we are concerned with designing a parallel algorithm that
must execute as part of a larger system. In this case, another
software engineering issue that must be considered is the data
distributions utilized by other program components. For example, the
best algorithm for some program component may require that an input
array data structure be decomposed in three dimensions, while a
preceding phase of the computation generates a two-dimensional
decomposition. Either one or both algorithms must be changed, or an
explicit restructuring phase must be incorporated in the computation.
Each approach has different performance characteristics. These issues
are discussed in Chapter 4.
We have now revised the partitioning and communication decisions
developed in the first two design stages by agglomerating tasks and
communication operations. We may have agglomerated tasks because
analysis of communication requirements shows that the original
partition created tasks that cannot execute concurrently.
Alternatively, we may have used agglomeration to increase computation
and communication granularity and/or to decrease software engineering
costs, even though opportunities for concurrent execution are reduced.
At this stage, we evaluate our design with respect to the following
checklist. Several of these questions emphasize quantitative
performance analysis, which becomes more important as we move from the
abstract to the concrete; this topic is addressed in
Chapter 3.
-
Has agglomeration reduced communication costs by increasing locality?
If not, examine your algorithm to determine whether this could be
achieved using an alternative agglomeration strategy.
-
If agglomeration has replicated computation, have you verified that
the benefits of this replication outweigh its costs, for a range of
problem sizes and processor counts?
-
If agglomeration replicates data, have you verified that this does not
compromise the scalability of your algorithm by restricting the range
of problem sizes or processor counts that it can address?
-
Has agglomeration yielded tasks with similar computation and
communication costs? The larger the tasks created by agglomeration,
the more important it is that they have similar costs. If we have
created just one task per processor, then these tasks should have
nearly identical costs.
-
Does the number of tasks still scale with problem size? If not, then
your algorithm is no longer able to solve larger problems on larger
parallel computers.
-
If agglomeration eliminated opportunities for concurrent execution,
have you verified that there is sufficient concurrency for current and
future target computers? An algorithm with insufficient concurrency
may still be the most efficient, if other algorithms have excessive
communication costs; performance models can be used to quantify these
tradeoffs.
-
Can the number of tasks be reduced still further, without introducing
load imbalances, increasing software engineering costs, or reducing
scalability? Other things being equal, algorithms that create fewer
larger-grained tasks are often simpler and more efficient than those
that create many fine-grained tasks.
-
If you are parallelizing an existing sequential program, have you
considered the cost of the modifications required to the sequential
code? If these costs are high, consider alternative agglomeration
strategies that increase opportunities for code reuse. If the
resulting algorithms are less efficient, use performance modeling
techniques to estimate cost tradeoffs.
![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)
Next: 2.5 Mapping
Up: 2 Designing Parallel Algorithms
Previous: 2.3 Communication
© Copyright 1995 by Ian Foster

![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)

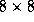 grid is partitioned
into
grid is partitioned
into 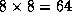 tasks, each responsible for a single point, while
in (b) the same computation is partioned into
tasks, each responsible for a single point, while
in (b) the same computation is partioned into 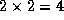 tasks, each
responsible for 16 points. In (a),
tasks, each
responsible for 16 points. In (a), 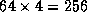 communications
are required, 4 per task; these transfer a total of 256 data values.
In (b), only
communications
are required, 4 per task; these transfer a total of 256 data values.
In (b), only 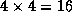 communications are required, and only
communications are required, and only
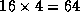 data values are transferred.
data values are transferred.
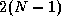 or
or 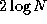 steps,
respectively, the sum of the N values is replicated in each of the
N tasks.
steps,
respectively, the sum of the N values is replicated in each of the
N tasks. steps,
depending on which communication structure is used
(Figure
steps,
depending on which communication structure is used
(Figure 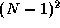 redundant additions and
redundant additions and 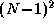 unnecessary communications. However, the summation and broadcast
complete in N-1
rather than 2(N-1)
steps. Hence, the
strategy is faster if the processors would otherwise be idle waiting
for the result of the summation.
unnecessary communications. However, the summation and broadcast
complete in N-1
rather than 2(N-1)
steps. Hence, the
strategy is faster if the processors would otherwise be idle waiting
for the result of the summation.
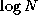 steps each task has
a copy of the sum. One might expect this approach to result in
steps each task has
a copy of the sum. One might expect this approach to result in
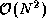 additions and communications, as in the ring algorithm.
However, in this case we can exploit redundancies in both computation
and communication to perform the summation in just
additions and communications, as in the ring algorithm.
However, in this case we can exploit redundancies in both computation
and communication to perform the summation in just 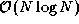 operations. The resulting communication structure, termed a
butterfly, is illustrated in Figure
operations. The resulting communication structure, termed a
butterfly, is illustrated in Figure 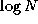 stages, each task receives data from two tasks, performs a
single addition, and sends the result of this addition to two tasks in
the next stage.
stages, each task receives data from two tasks, performs a
single addition, and sends the result of this addition to two tasks in
the next stage.

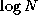 steps. Numbers located
in the bottom row of tasks are propagated up through
steps. Numbers located
in the bottom row of tasks are propagated up through  intermediate stages, thereby producing the complete sum in each task
in the top row.
intermediate stages, thereby producing the complete sum in each task
in the top row.